np.trsnspose() (p536)

この関数が行っている行列の変換の仕方が分かりづらかった。

本書よりもっと単純な行列でその変換の仕方を見る。

import numpy as np
n1 = np.arange(1,13,1)
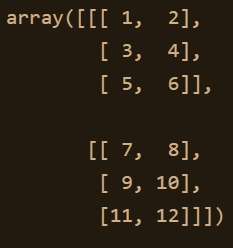
n2 = n1.reshape(2,3,2)
n2

array([[[ 1,  2],
        [ 3,  4],
        [ 5,  6]],

       [[ 7,  8],
        [ 9, 10],
        [11, 12]]])

この行列をnp.transpose関数で変換してみると

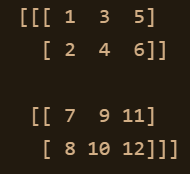
n3 = np.transpose(n2, (0,2,1))
print(n3)
n3.shape

[[[ 1  3  5]
  [ 2  4  6]]

 [[ 7  9 11]
  [ 8 10 12]]]

(2, 2, 3)

正直言うと、この変換がどのような法則で行われているのかわからなかった。公式ドキュメントにはこの変換で軸を入れ替えると書いてあるが、それは分かるのである。実際にこの変換がどのような法則によって行われているのか、自分なりにかみ砕いて説明する。

▪ 3段階で変換

変換は3段階に分けて考えると分かりやすい。

全体の構造を把握
一番内側の（最小の）格子 [] の中身が、元の行列のどの部分に相当するか
次に来る格子が、元の行列のどの部分に相当するか

である。具体的に上の例ではどういうことなのかは以下の通り

n3.shapeで構造を確認
新しくできた行列の[1,3,5]がどのようにして生成されたかを考える。
新しくできた行列の[2,4,6]がどのように生成されたかを考える。

▪ 最初に生成される格子は何か

もう少し具体的に説明する。

1．については簡単で、n3.shapeの結果を見ればよいが2．が難しい。2．では「一番最初に生成される格子が何なのか」という事に注目しているが、この際大切なのは行列の最小単位を決定する部分はどこかなので、np.transpose(a,b,c)のcに注目すると良い。今回の場合、np.transpose(0,2,1)なので、1に注目する。この軸１は元の行列で何を示しているのだろうか。

今回大事なのは（元の行列において）1,3,5の（縦）方向で行列を作るという意味であると思う。

▪1,3,5の（縦）方向で行列を作るとは

それを考える前に思い出したいのは、今の目標は「なぜ新しく生成された最初の格子が[1,3,5]になったのか」の解明、という事だ。1．で得られた構造も参考にすると、新しくできる行列の形は（2,2,3）であり、何か3つの数を取り出せば最小格子の中身が得られるという事は簡単に読み取れる。

そしてその「何か3つの数」をどのようにして取り出すか、それが1,3,5の（縦）方向であるという事なのだ。すなわち、新たな行列の最小格子の一つは[1,3,5]であると分かる。

---縦並べ比較---

▪ 2つ目に生成される格子は何か

新たな行列では[2,4,6]が次に来ている。これはどういうことなのかというのが、3．で分かるようになっている。

先ほどと同じ要領で、とりあえず[2,4,6]か[7,9,11]を取り出せば良いという事は何となくわかるはずである。では、どちらが正解なのか。

▪ 2つ目の格子の取り出し方

次に来る格子を判断するためにはnp.transpose(a,b,c)のbに注目すると良い。これが次の格子を選ぶ際の軸となる。今回はnp.transpose(0,2,1)なので、2に注目する。軸2について大切なのは（元の行列において）1,2や3,4方向で数えるという意味だけである。このように数え方の方向性が分かれば、元の行列から[1,3,5]の次に取ってくる格子の中身は、1,2方向（横方向）に進んで[2,4,6]にすると理解することが出来るはずである。決して[7,9,11]ではないという事だ。

新たにできる行列の形は（2,2,3）なので、以上で（2,3）の1セットは完成である。これをもう1セット作れば、新たな行列の完成だ。

ちなみに、np.transpose(0,1,2)の0はあまり気にしなくても何とかなるというのが今のところの感想で、大事なのはその後ろの2つの軸であるという事を覚えておきたい。

▪ 本の例で確認してみる

以下が、本書のnp.transposeの変換である。

n4 = np.arange(0,24,1)
n5 = n4.reshape(2,3,4)
print(f'n5のshapeは {n5.shape}で、中身は以下の通り')
print(n5)

n5のshapeは (2, 3, 4)で、中身は以下の通り
[[[ 0  1  2  3]
  [ 4  5  6  7]
  [ 8  9 10 11]]

 [[12 13 14 15]
  [16 17 18 19]
  [20 21 22 23]]]

n6 = np.transpose(n5,(1,2,0))
print(f'n6のshapeは{n6.shape}で、中身は以下の通り')
print(n6)

n6のshapeは(3, 4, 2)で、中身は以下の通り
[[[ 0 12]
  [ 1 13]
  [ 2 14]
  [ 3 15]]

 [[ 4 16]
  [ 5 17]
  [ 6 18]
  [ 7 19]]

 [[ 8 20]
  [ 9 21]
  [10 22]
  [11 23]]]

また説明するのは大変なので例を載せて終了にするが、分かっただろうか。先ほどと同じように、出来る最小格子は[0,12]や[1,13]や[4,16]などだと分かれば、あとは何とかなるはずである。

『pytorch ＆深層学習プログラミング』　入門編

目次